Question

A marketing consultant observed 50 consecutive shoppers at a supermarket. One variable of interest was how much each shopper spent in the store. Here are the data (in dollars), arranged in increasing order.

5.24 11.97 13.59 15.52 15.69 19.96 20.54 22.59 27.25 27.29
28.25 30.00 31.63 33.01 37.21 40.36 40.90 42.83 45.66 46.67
47.49 49.32 50.12 51.71 52.21 53.57 56.16 56.36 56.88 58.65
59.42 60.20 60.48 62.23 62.50 67.95 70.45 73.08 74.15 74.48
74.78 75.75 76.27 76.47 78.92 84.09 84.91 85.06 88.45 88.91

a. What is the mean amount a customer spends at the grocery store?
b. Assume that the standard deviation is $20.00. Find a 95% confidence interval for the mean amount spent by shoppers in similar circumstances.

Answer 1

a.
`\\ \mu = USD\;51.34`; b. The 95% interval is USD [45.82, 56.86].

Explanation:

The mean amount a customer spends at the grocery store

The mean is the sum of all of the data divided by the number of observations for this case, that is, n = 50.

The sum of all of the data is: 5.24+11.97+13.59+15.52+15.69+19.96+20.54+22.59+27.25+27.29+28.25+30.00+31.63+33.01+37.21+40.36+40.90+42.83+45.66+46.67+47.49+49.32+50.12+51.71+52.2 1+53.57+56.16+56.36+56.88+58.65+59.42+60.20+60.48+62.23+62.50+67.95+70.45+73.08+74.15+74.48+74.78+75.75+76.27+76.47+78.92+84.09+84.91+85.06+88.45+88.91 = 2567.17.

The mean
`\\ \mu` is

`\\ \mu = (2567.17)/(50)`

`\\ \mu = (2567.17)/(50) = 51.34`

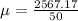
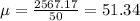
Then, the mean amount a customer spends at the grocery store is USD 51.34.

The 95% confidence interval for the mean amount spent

For the 95% confidence interval for the mean, we have the value for the mean = 51.34, as we have just found, the value for the standard deviation is already given as USD 20.00. There are 50 observations, so n = 50.

Moreover, for a 95% confidence, the value for the corresponding z-score is z = 1.96 (this is the confidence coefficient). Then, the formula for finding the "limits" values for the confidence interval is as follows:

For the upper limit

`\\ \overline{X} + 1.96*(\sigma)/(√(n))`

`\\ 51.34 + 1.96*(20)/(√(50))`

`\\ 51.34 + 5.52`

`\\ 56.86`

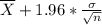
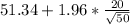
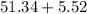
For the lower limit

`\\ \overline{X} - 1.96*(\sigma)/(√(n))`

`\\ 51.34 - 1.96*(20)/(√(50))`

`\\ 51.34 - 5.52`

`\\ 45.82`

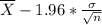
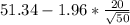
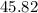
Thus

The 95% confidence is USD [45.82, 56.86].

Mathematically

`\\ P(45.82 \leq \mu \leq 56.86) = 0.95`

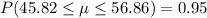
There is a probability of 0.95 that the values are between [45.82, 56.86], both inclusive.

We have to remember here that we are dealing with a sample. This sample has a standard deviation, called standard error of the sample, and is
`\\ (20)/(√(50)) \approx 2.83`.

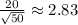So, the population mean is, with a 95% confidence, between the values [45.82, 56.86], both inclusive.

We can see the graph below that represents the former.