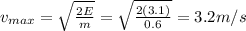Question

A horizontal spring-mass system has low friction, spring stiffness 165 N/m, and mass 0.6 kg. The system is released with an initial compression of the spring of 7 cm and an initial speed of the mass of 3 m/s.

(a) What is the maximum stretch during the motion?
(b) What is the maximum speed during the motion?

Answer 1

a) 19.4 cm

b) 3.2 m/s

Step-by-step explanation:

a)

A horizontal spring-mass system has a motion called simple harmonic motion, in which the mass oscillates following a periodic function (sine or cosine) around an equilibrium position.

As the system oscillates back and forth, its total mechanical energy (sum of elastic potential energy and kinetic energy) will remain conserved (since we consider friction negligible). The elastic potential energy at any point is given by:

`U=(1)/(2)kx^2`

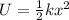
where

k is the spring constant

x is the displacement of the system

While the kinetic energy at any point is

`K=(1)/(2)mv^2`

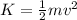
where

m is the mass

v is the speed

So the total mechanical energy of the system is

`E=K+U=(1)/(2)mv^2+(1)/(2)kx^2`

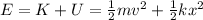
For this system, when it is initially released,

m = 0.6 kg

k = 165 N/m

x = 7 cm = 0.07 m

v = 3 m/s

So the total energy is

`E=(1)/(2)(0.6)(3)^2+(1)/(2)(165)(0.07)^2=3.1 J`

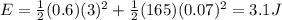
Since friction is negligible, this total energy remains constant. Therefore, when the system reaches its maximum stretch during the motion, the kinetic energy will be zero and all the mechanical energy will be elastic potential energy; so we will have:

`E=U=(1)/(2)kx_(max)^2`

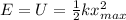
where
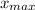`x_(max)` is the maximum stretch. Solving for
`x_(max)`,

`x_(max)=\sqrt{(2E)/(k)}=\sqrt{(2(3.1))/(165)}=0.194 m`

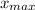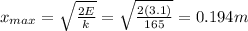
So, 19.4 cm.

b)

The maximum speed in a spring-mass oscillating system is reached when the kinetic energy is maximum, and therefore, since the total energy is conserved, when the elastic potential energy is zero:

`U=0`

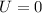
which means when the displacement is zero:

x = 0

So, when the system is transiting through the equilibrium position.

Therefore, the total mechanical energy is equal to the maximum kinetic energy:

`E=K=(1)/(2)mv_(max)^2`

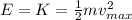
where

m is the mass

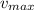`v_(max)` is the maximum speed

Here we have:

E = 3.1 J

m = 0.6 kg

Therefore, solving for the maximum speed,

`v_(max)=\sqrt{(2E)/(m)}=\sqrt{(2(3.1))/(0.6)}=3.2 m/s`