Question

Which sequence could be partially defined by the recursive formula f (n + 1) = f(n) + 2.5 for n ≥ 1?

2.5, 6.25, 15.625, 39.0625, …
2.5, 5, 10, 20
–10, –7.5, –5, –2.5, …
–10, –25, 62.5, 156.25

Answer 1

It's c bruv

Step-by-step explanation:

It's c boy

Answer 2

Option C: –10, –7.5, –5, –2.5, … is the sequence.

Step-by-step explanation:

The given recursive formula is
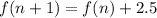`f(n+1)=f(n)+2.5` for
`n\geq 1`

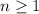
We need to determine the sequence.

The sequence can be determined by substituting n = 1, 2, 3, 4,....

And
`f(1)=-10`

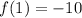
2nd term of the sequence:

Substituting n = 1 in the formula
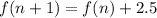`f(n+1)=f(n)+2.5`, we get,

`f(1+1)=f(1)+2.5`

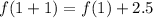
Simplifying, we have,

`f(2)=-10+2.5=-7.5`

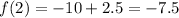
Thus, the 2nd term of the sequence is -7.5

3rd term of the sequence:

Substituting n = 2 in the formula
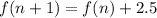`f(n+1)=f(n)+2.5`, we get,

`f(2+1)=f(2)+2.5`

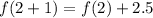
Simplifying, we have,

`f(3)=-7.5+2.5=-5`

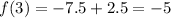
Thus, the 3rd term of the sequence is -5

4th term of the sequence:

Substituting n = 3 in the formula
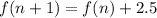`f(n+1)=f(n)+2.5`, we get,

`f(3+1)=f(3)+2.5`

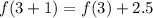
Simplifying, we have,

`f(4)=-5+2.5=-2.5`

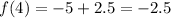
Thus, the 4th term of the sequence is -2.5

Therefore, the sequence is –10, –7.5, –5, –2.5, …

Hence, Option C is the correct answer.