Answer:
The sample size used to compute the 95% confidence interval is 1066.
Explanation:
The (1 - α)% confidence interval for population proportion is:
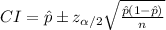
The 95% confidence interval for proportion of the bank's customers who also have accounts at one or more other banks is (0.45, 0.51).
To compute the sample size used we first need to compute the sample proportion value.
The value of sample proportion is:
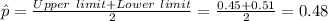
Now compute the value of margin of error as follows:
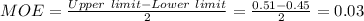
The critical value of z for 95% confidence level is:
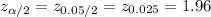
Compute the value of sample size as follows:
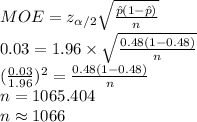
Thus, the sample size used to compute the 95% confidence interval is 1066.