Question

Consider the following problem: A farmer with 950 ft of fencing wants to enclose a rectangular area and then divide it into four pens with fencing parallel to one side of the rectangle. What is the largest possible total area of the four pens

Answer 1

Largest possible total area of the four pens is
`22562.5\:ft^(2)`

Explanation:

Assume width as x and length as y. Given that length of fencing is 950 feet which encloses rectangular area which is divided into four pens as shown in diagram ( Refer to attachment),

So perimeter of the rectangular area as per diagram is given as,

Perimeter = width + width + width + width + width + length+ length

Substituting the value,

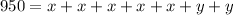`950=x+x+x+x+x+y+y` ….1

Now area of rectangular diagram is given as follows,

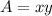`A=xy` ….2

Solving equation 1 for y, subtracting 2x from both sides,

`(950-5x)/(2)= y`

`475-(5x)/(2)= y`

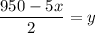
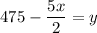
Substituting the value in equation 2,

`A=x\left(475-(5x)/(2)\right)`

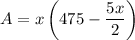
Simplifying

`A=475x-(5x^(2))/(2)`

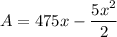
To find the largest possible area, differentiate A with respect to x,

`(dA)/(dx)=(d)/(dx)\left(475x-(5x^(2))/(2)\right)`

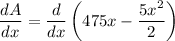
Applying sum rule of derivative,

`(dA)/(dx)=(d)/(dx)\left(475x\right)-(d)/(dx)\left((5x^(2))/(2)\right)`

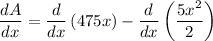
Applying constant multiple rule of derivative,

`(dA)/(dx)=475(d)/(dx)\left(x\right)-(5)/(2)(d)/(dx)\left(x^(2)\right)`

Applying power rule of derivative,

`(dA)/(dx)=475\left(1x^(1-1)\right)-(5)/(2)\left(2x^(2-1)\right)`

`(dA)/(dx)=475\left(x\right)-(5)/(2)\left(2x\right)`

`(dA)/(dx)=475-5x`

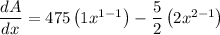
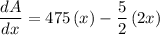
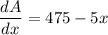
Now find the critical number by solving as follows,

`(dA)/(dx)=0`

`475-5x =0`

`475=5x`

`95=x`

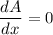
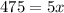
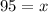
Since there is only one critical point, directly substitute the value of x into equation of A,

`A=475\left(95\right)-(5\left(95\right)^(2))/(2)`

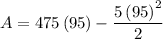
Simplifying,

`A=45125-(45125)/(2)`

`A=(45125)/(2)`

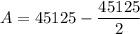
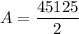
So, the largest possible area is
`22562.5\:ft^(2)`