Question

A bottle in lab is labeled [CoCl2.6H2O] = 0.652 M in 8.433 M HCl. If you determine [CoCl42-] to be 0.129 M at a particular temperature using absorbance measurements, what must be the value of [Co(H2O)62+] in the solution at that temperature?

Answer 1

Step-by-step explanation:

Chemical equation for the given reaction is as follows.

`[Co(H_(2)O)_(6)]^(2) + 4Cl^(-) \rightleftharpoons [CoCl_(4)]^(2-) + 6H_(2)O`

First, we will calculate the moles of
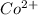`Co^(2+)` as follows.

`(0.652 * 1 mole Co^(2+))/(1 mole [CoCl(H_(2)O)_(6)]^(2+))`

= 0.652 mol
`Co^(2+)`

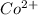
Therefore,

`(0.129 * 1 mole Co^(2+))/(1 mol of CoCl^(2-)_(4))`

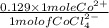
= 0.129 moles of
`Co^(2+)`

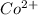
Now, moles per liter of
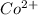`Co^(2+)` which will not react will be calculated as follows.

0.652 - 0.129

= 0.523

Thus, we can conclude that there are 0.523 moles of
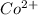`Co^(2+)`present per liter.