Question

Two metal balls are the same size but one weighs twice as much as the other. The balls are dropped from the roof of a single story building at the same instant of time. The time it takes the balls to reach the ground below will be: (A) about half as long for the heavier ball as for the lighter one. (B) about half as long for the lighter ball as for the heavier one. (C) about the same for both balls. (D) considerably less for the heavier ball, but not necessarily half as long. (E) considerably less for the lighter ball, but not necessarily half as long.

Answer 1

C) about the same for both balls

Step-by-step explanation:

When two metal balls of same size are dropped from the same height at the same instance of time then the time taken by both the balls to reach the ground will be same because there acts almost equal net force on both the balls.

As we know that the net velocity of a free falling object is independent of its mass.

`v=√(2g.h)`

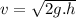
where:

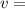`v=` final velocity of the falling object just before impacting the ground

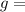`g=` acceleration due to gravity

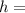`h=` height of fall

Also by using the equation of motion:

`h=u.t+(1)/(2)g.t^2`

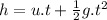
where:

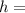`h=` height of fall

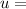`u=` initial velocity of the object during the course of motion

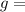`g=` acceleration due to gravity

t = time taken

we find that the time taken is independent of the mass of the object.

Also the drag force acting in the opposite direction to the motion is given as:

`F_d=(1)/(2) \rho.A.v^2.c_d`

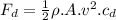
where:

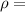`\rho=` density of air

`A=` area subjected normal to the velocity

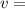`v=` velocity of the object

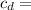`c_d=` coefficient of drag

Since the balls are of same size the drag force is also nearly equal hence the time taken to fall the same height will be equal.