Question:
The amount of cereal that can be poured into a small bowl varies with a mean of 1.5 ounces and a standard deviation of 0.3 ounces. A large bowl holds a mean of 2.5 ounces with a standard deviation of 0.4 ounces. You open a new box of cereal and pour one large and one small bowl.
Answer:
a) The expected amount of cereal left in the box is 12.2 ounces
b) The standard deviation
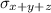 , is 0.5099
, is 0.5099
c) In a Normal model, the probability that the box still contains more than 13 ounces is P(Z-(X+Y) > 13) = 5.821 %.
Explanation:
Let X represent the amount of cereal that can be poured into a small bowl and Y represent the amount of cereal that can be poured into a large bowl and Z represent the amount of cereal that the manufacturer puts in the box, then the expected amount of cereal left in the box is given by
Z - (X + Y)
(a) The expected amount of cereal left in the box is given as
P(Z - (X + Y)) = μ = μ
 - μ
- μ
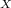 - μ
- μ
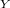 = 16.2 - 1.5 - 2.5 = 12.2 ounces
= 16.2 - 1.5 - 2.5 = 12.2 ounces
The expected amount of cereal left in the box = 12.2 ounces
b) The standard deviation is given by the root of the sum of the variance
That is
 and
and
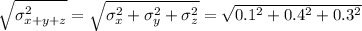 = 0.5099
= 0.5099
The standard deviation,
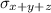 , = 0.5099
, = 0.5099
c) The probability that the box still contains more than 13 ounces is given by
P(Z-(X+Y) > 13)
Where z-score is
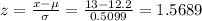 ≈ 1.57
≈ 1.57
From the z-score table P(Z = 1.57) = 0.94179
Therefore the probability of the box containing ≤ 13 is 0.94179, that is
P(Z-(X+Y) ≤ 13) = 0.94179 and
P(Z-(X+Y) > 13) = 1 - 0.94179 = 0.05821 = 5.821 %.