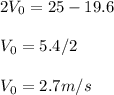Question

A ball is thrown at the ground from the top of a tall building. The speed of the ball in meters per second is v(t)=9.8t+v0, were t denoted the number of seconds since the ball has been thrown and v0 is the initial speed of the ball. If the ball travels 25 meters during the first 2 seconds after it is thrown, what was the initial speed of the ball?

Answer 1

`V_0=2.7m/s`

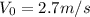
Step-by-step explanation:

The speed of the ball in meters per second is

`V(t)=9.8t+V_0`

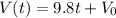
Where t denotes the number of seconds since the ball has been thrown and
`V_0` is the initial speed of the ball. Then:

`V(2)=9.8(2)+V_0\\\\V(2)=19.6+V_0`

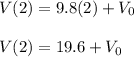
If the ball travels 25 meters during the first 2 seconds after it is thrown, what was the initial speed of the ball

Also, for constant acceleration motion, the average velocity is equal to the sum of final and initial velocities divided by 2 and to the distance divided by the time:

`(V(t)+V_0)/(2)=(d)/(t)`

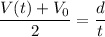
Where you know:

• t = 2s

• 
  `V(2)=9.8(2)+V_0=19.6+V_0`

• d = 25m

Substituting (the units are ommited in the equationn, but added at end of the answer):

`(V(2)+V_0)/(2)=(25)/(2)`

`V(2)+V_0=25`

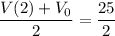
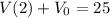
Thus, you have a system of equations:

`V(2)+V_0=25`

`V(2)=19.6+V_0`

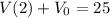
Substituting the second into the first:

`19.6+V_0+V_0=25\\\\19.6+2V_0=25`

`2V_0=25-19.6\\\\V_0=5.4/2\\\\V_0=2.7m/s`