Answer:
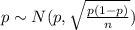
And the parameters are given by:
The mean is given by:
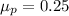
The standard deviation is:

And the distribution would be bell shaped and normal
Explanation:
For this case we have the following info given :
p =0.25 represent the proportion of BYU-Idaho students that are married
n = 100 represent the sample size
And for this case we can check the conditions in order to use the normal distribution:
1) np = 100*0.25 = 25>10
2) n(1-p) =100*(1-0.25)= 75>10[/tex]
3) Independence is assumed in each sample and the probability is the same
So then we have all the conditions satisfied, and the distribution for the proportion would be given by:
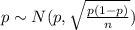
And the parameters are given by:
The mean is given by:
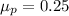
The standard deviation is:

And the distribution would be bell shaped and normal