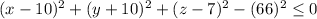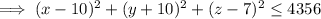Answer:
Equation of solid ball is
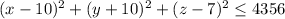 .
.
Explanation:
A equation of a solid ball centered at (a,b,c) with radious r is of the form,
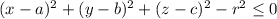
Here
 takes the inner region and outer surfaces of the solid. So in this problem center (a,b,c)=(10,-10,-7) and radious r=66, then equation of required solid ball is,
takes the inner region and outer surfaces of the solid. So in this problem center (a,b,c)=(10,-10,-7) and radious r=66, then equation of required solid ball is,