Question

AA, BBB, and CCC are collinear, and BBB is between AAA and CCC. The ratio of ABABA, B to ACACA, C is 1:31:31, colon, 3. If AAA is at (-2,-3)(−2,−3)left parenthesis, minus, 2, comma, minus, 3, right parenthesis and BBB is at (-6,-1)(−6,−1)left parenthesis, minus, 6, comma, minus, 1, right parenthesis, what are the coordinates of point CCC?

Answer 1

The co-ordinate of C is (0,-4).

Explanation:

Given that , points A, B and C are collinear.

If all points lie in a same line, then the points are called co-linear.

The ratio AB to AC is 1:3.

It means the point A divided the line BC in ratio 1:3 externally.

The co-ordinate of A is (-2,-3) and the co-ordinate of B is (-6,-1).

If a line joining by two points (x₁,y₁) and (x₂,y₂) is divided by a point in the ratio m:n externally, then the co-ordinate of the point is

`(\frac {mx_2-nx_1}{m-n},\frac {my_2-ny_1}{m-n})`

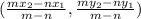
Here x₁= -2,y₁= -3, x₂= -6,y₂= -1 and m=1 and n = 3

The co-ordinate of C is

`((1.(-6)-3(-2))/(1-3),(1.(-1)-3(-3))/(1-3))`

`=((-6+6)/(-2),(-1+9)/(-2))`

`=(0,(8)/(-2))`

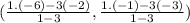
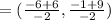
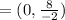
=(0,-4)