Question

Consider the following equations. x = 1 − t2, y = t − 5, −2 ≤ t ≤ 2 (a) Sketch the curve by using the parametric equations to plot points. Indicate with an arrow the direction in which the curve is traced as t increases.

Answer 1

A parable opened to the left!

Explanation:

Easy, easy!

Well, if you can draw!!!

First, the parameter is t!

So for each value of t, there is a value for x and y!

That is if t=-2, x=-3 and y=-7 because x=1-(2)^2= 1-4=-3, and y=(-2)-5=-7.

Then we take the next values for t and get x and y

t= -2, -1, 0, 1, 2

x= -3, 0, 1, 0, -3

y= -7, -6, -5, -4, -3,

As you can see in the graphics, there are many other point in order to get a very clear view. The result is parable that opens its arms to the left starting from the bottom left, at the point (-3,-7) at t=-2, then goes to the upright until the point (1,-5), at t=0, then goes back to the left keeping upward until the point (-3,-3), at t=2.

Answer 2

See graph attached.

The path of the curve, as t increases goes from the top of the curve going down, following a parabola symmetric in y=5.

Explanation:

We have the following parametrics equations:

`x=1-t^2\\\\y=t-5\\\\-2\leq t \leq 2`

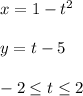
We can graph the variables x and y in a xy-plane following the values of t within the interval defined.

To do that we compute the values for x and y for every t in the interval and graph it.

The path of the curve, as t increases goes from the top of the curve going down, following a parabola symmetric in y=5.