Answer:
Change in area=24
 -48
-48
Explanation:
Let s will be the side of square and r will be the radius of circle.
Then two given conditions are
1)dr/dt=2 m/s
2)ds/dt=1 m/s
Area enclosed=(Area of square)-(Area of circle)
Area of square=

Area of circle=

Area enclosed=
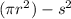
dA/dt=2
 r(dr/dt)-2s(ds/dt)
r(dr/dt)-2s(ds/dt)
At s=24,and r=6
dA/dt=2(
 )(6)(2)-2(24)(1)
)(6)(2)-2(24)(1)
Change in area=24
 -48
-48