The sum of the digits of a 2-digit number is 11. If the digits are reversed, the number formed is 45 more than the original number. Find the original number. If x is the ten…

Question

asked Aug 10, 2021 232k views

2 Answers

Denis Tsoi · Answer 1 · 2021-08-17T11:20:45+0000

The original number is 38

Step-by-step explanation:

Let the sum of the digits of a 2 digit number is 11.

If the digits are reversed, the number formed is 45 more than the original number.

Let x and y be the two numbers and
x+y=11

Let the original number be
10x+y

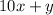
Let the reversed number be
10y+8

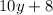
We need to determine the original number.

Original number:

We need to determine the original number
10x+y

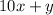
Thus, we have,

x+y=11 -----(1)

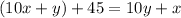(10x+y)+45=10y+x --------(2)

Solving the equation (2), we get,

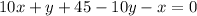
10x+y+45-10y-x=0

9x-9y=-45

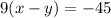
9(x-y)=-45

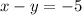x-y=-5 --------(3)

Adding the equations (1) and (3), we get,

2x=6

x=3

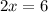
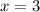
Thus, the value of x is 3

Substituting
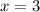x=3 in equation (1), we get,

3+y=11

y=8

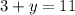
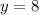
Thus, the value of y is 8.

The equation of the original number is
10x+y

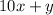
Substituting the value of x and y, we get,

Original number =
$10(3)+8\implies 30+8=38$

Thus, the original number is 38.