1 Answer

Apoorv Verma · Answer 1 · 2021-11-27T12:51:24+0000

Option D:
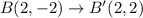$B(2,-2) \rightarrow B^(\prime)(2,2)$ is the pair of points which does not have y - axis as the line of reflection.

Step-by-step explanation:

The translation rule to reflect the pair of points across the y - axis is given by

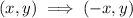
$(x,y)\implies (-x,y)$

Option A:
$B(3,-8) \rightarrow B^(\prime)(-3,-8)$ :

Let us translate the coordinate B(3,-8) across y - axis using the translation rule
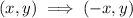$(x,y)\implies (-x,y)$ , we get,

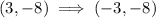
$(3,-8)\implies (-3,-8)$

Thus, we get,
$B(3,-8) \rightarrow B^(\prime)(-3,-8)$

Hence, the pair of points
$B(3,-8) \rightarrow B^(\prime)(-3,-8)$ has the line of reflection across y - axis.

Therefore, Option A is not the correct answer.

Option B:
$B(-6,2) \rightarrow B^(\prime)(6,2)$ :

Let us translate the coordinate B(-6,2) across y - axis using the translation rule
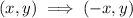$(x,y)\implies (-x,y)$ , we get,

$(-6,2)\implies (6,2)$

Thus, we get,
$B(-6,2) \rightarrow B^(\prime)(6,2)$

Hence, the pair of points
$B(-6,2) \rightarrow B^(\prime)(6,2)$ has the line of reflection across y - axis.

Therefore, Option B is not the correct answer.

Option C:
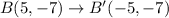$B(5,-7) \rightarrow B^(\prime)(-5,-7)$ :

Let us translate the coordinate B(5,-7) across y - axis using the translation rule
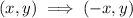$(x,y)\implies (-x,y)$ , we get,

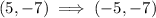
$(5,-7)\implies (-5,-7)$

Thus, we get,
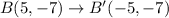
$B(5,-7) \rightarrow B^(\prime)(-5,-7)$

Hence, the pair of points
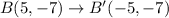$B(5,-7) \rightarrow B^(\prime)(-5,-7)$ has the line of reflection across y - axis.

Therefore, Option C is not the correct answer.

Option D:
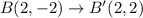$B(2,-2) \rightarrow B^(\prime)(2,2)$ :

Let us translate the coordinate B(2,-2) across y - axis using the translation rule
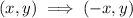$(x,y)\implies (-x,y)$ , we get,

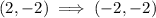
$(2,-2)\implies (-2,-2)$

Thus, we get,
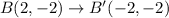
$B(2,-2) \rightarrow B^(\prime)(-2,-2)$

Hence, the pair of points
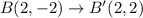$B(2,-2) \rightarrow B^(\prime)(2,2)$ does not has the line of reflection across y - axis.

Therefore, Option D is the correct answer.

Please log in or register to add a comment.