Step-by-step explanation:
Here we have the following expression:
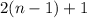
So we can rewrite this as follows:
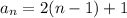
So this is an arithmetic series whose general form is given by:
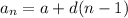
Where:
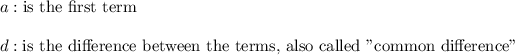
So, for some n-values we have:

From this information, the diagram that best represents the given expression is shown below.