The rate of change of the linear function is
 .
.
Explanation:
To find the rate of change for the given function, we have to do some reverse operations. We have to rewrite the equation in the form of y = mx+ b where m is the slope or rate of change of the given function and b is the y - intercept for the given function. Now we have to rewrite the equation as,
9x - 2y = -10
Adding -9x on both sides, we will get,
9x-9x -2y = -10 -9x
On LHS, 9x gets cancelled.
-2y = -9x-10
Then dividing both sides of the equation by -2, we will get,
y =

y =
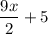
So the rate of change is
 .
.