Question

A random sample of 144 observations has a mean of 20, a median of 21, and a mode of 22. The population standard deviation is known to equal 4.8. The 95.44% confidence interval for the population mean is _____.

Answer 1

95.44% confidence interval for the population mean is [19.2 , 20.8].

Explanation:

We are given that a random sample of 144 observations has a mean of 20, a median of 21, and a mode of 22. The population standard deviation is known to equal 4.8.

Also, assuming that the data follows normal distribution.

So, the pivotal quantity for 95.44% confidence interval for the population mean is given by;

P.Q. =
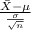`(\bar X - \mu)/((\sigma)/(√(n) ) )` ~ N(0,1)

where,
`\bar X` = sample mean = 20

`\sigma` = population standard deviation = 4.8

n = sample of obs. = 144

`\mu` = population mean

So, 95.44% confidence interval for the population mean,
`\mu` is ;

P(-1.9991 < N(0,1) < 1.9991) = 0.9544

P(-1.9991 <
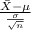`(\bar X - \mu)/((\sigma)/(√(n) ) )` < 1.9991) = 0.9544

P(
`-1.9991 * {(4.8)/(√(144) )` <
`{\bar X - \mu}` <
`1.9991 * {(4.8)/(√(144) )` ) = 0.9544

P(
`\bar X - 1.9991 * {(\sigma)/(√(n) )` <
`\mu` <
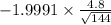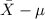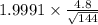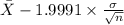`\bar X + 1.9991 * {(\sigma)/(√(n) )` ) = 0.9544

95.44% confidence interval for
`\mu` = [
`\bar X - 1.9991 * {(\sigma)/(√(n) )` ,
`\bar X + 1.9991 * {(\sigma)/(√(n) )` ]

= [
`20 - 1.9991 * {(4.8)/(√(144) )` ,
`20 + 1.9991 * {(4.8)/(√(144) )` ]

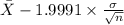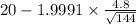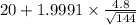= [19.2 , 20.8]

Therefore, 95.44% confidence interval for the population mean is [19.2 , 20.8].