Answer:
Point
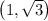 lies inside the circle.
lies inside the circle.
Explanation:
To determine the point which lies outside the circle, calculate the distance between the points and compare that value with radius of circle.
If d<r point lies inside the circle, d>r point lies outside circle and d=r point is on the circle.
Let O be the center of origin of the circle. So,
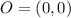 .
.
Also given that circle contain point
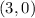 . So,
. So,
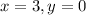
Now equation of circle having center (h,k) is given by the equation,
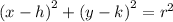

Substituting the value,
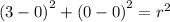
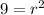
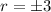
Now calculate the distance between point
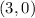 and
and
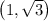 .
.
Distance formula between points
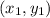 and
and
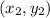 is given as,
is given as,
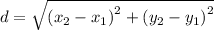
Now,
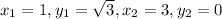
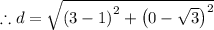
Simplifying,
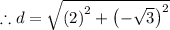
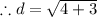
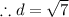

Since r = 3 and d = 2.64. That is, d < r.
So point
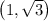 lies inside the circle.
lies inside the circle.