Question

Water (10 degree C) is flowing at a rate of 0.35 m^3/s, and it is assumed that h_L = 2 V^2/2g from the reservoir to the gage, where V is the velocity in the 30-cm pipe. What power must the pump supply? Assume alpha = 1.0 at all locations.

Answer 1

61.6 kw

Step-by-step explanation:

Q= 0.35 m^3/s ( flow rate )

Hl =
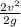`(2v^(2) )/(2g)` ( head loss)

D = 30 cm = 0.3 m ( diameter of pipe )

∝ = 1

A = area

first we find the V ( velocity )

V = Q / A =
`(0.35)/((\pi )/(4)(0.3)^(2) ) = 4.95 m/s`

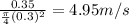
Hl =
`(2*(4.95)^(2) )/(2*9.81) = 2.497 m`

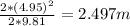
to calculate Hp apply the energy equation between water surface tank and the outlet of pipe neglecting pressure head of velocity head

The pipe will be :

Hp = (P1/y) + (V2^2/2g) + Zs + Hl

= (100*10^3 / 9810 ) + (4.95^2 / 2*9.81 ) + ( 10-6 ) + ( 2.497 )

= 17.939 m

to calculate the power the pump must supply we apply the power equation

P = yQHp

= 9810 * 0.35 * 17.939

= 61.6 kw

y = 9810 (constant)