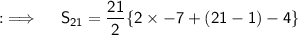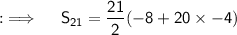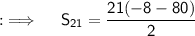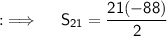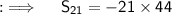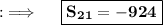Question

Find the sum of the first 21 terms of the arithmetic progression.
−7, −11, −15, . . .

Answer 1

We are given with an AP (Arithmetic Progression) with first term being -7, and the common difference being the difference between any succeding term from any term and the term itself, so common difference = -11 - (-7) = -11 + 7 = -4, so now before finding the sum of 21 terms, let's recall that ;

• 
  `{\boxed{\bf{S_(n)=(n)/(2)\{2a+(n-1)d\}}}}`

Where, d is the common difference, a is the first term, and n is the number of terms and
`{\bf S_n}`, being the sum of n terms, so putting all the values in the formula, we will have ;

`{:\implies \quad \sf S_(21)=(21)/(2)\{2* -7+(21-1)-4\}}`

`{:\implies \quad \sf S_(21)=(21)/(2)(-8+20* -4)}`

`{:\implies \quad \sf S_(21)=(21(-8-80))/(2)}`

`{:\implies \quad \sf S_(21)=(21(-88))/(2)}`

`{:\implies \quad \sf S_(21)=-21* 44}`

`{:\implies \quad \boxed{\bf{S_(21)=-924}}}`