Question

Find the volume of material remaining in a hemisphere of radius 2 after a cylindrical hole ofradius 1 is drilled through the center of the hemisphere perpendicular to its base.

Answer 1

Explanation:

Inicially we have to separate the sphere into 3 parts:

The donut + 1 ball cap (or a dome) + the cylinder hole = the Hemisphere

vide picture

As it shows in the picture we have to find the donut.

The donut = the Hemisphere - ( 1 dome + the cylinder hole)

• The hemisphere =
  `(4*pi*r^(3) )/(6)` (from the hemisphere formula)
• 1 dome* =
  `(1)/(6)*pi*(r-\sqrt{(r^(2) -a^(2)})*(3a^(2)+((r-\sqrt{(r^(2) -a^(2)})^(2) )`
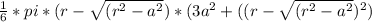
• cylinder hole =
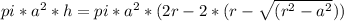  `pi*a^(2)*h = pi*a^(2) *(2r - 2*(r-\sqrt{(r^(2) -a^(2)}))` (h: cylinder height)

`D = (4*pi*r^(3) )/(6) - ((1)/(6)*pi*(r-\sqrt{(r^(2) -a^(2)})*(3a^(2)+((r-\sqrt{(r^(2) -a^(2)})^(2) )+ pi*a^(2)*(2r - 2*(r-\sqrt{(r^(2) -a^(2)})) }`

`D = (4*pi*2^(3) )/(6) - ((1)/(6)*pi*(2-\sqrt{(2^(2) -1^(2)})*(3*1^(2)+((2-\sqrt{(2^(2) -1^(2)})^(2) )+ pi*1^(2)*(2*2 - 2*(2-\sqrt{(2^(2) -1^(2)})) }`

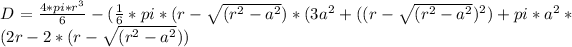
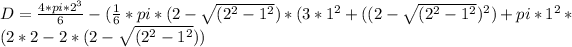
By basic algebra we have

D = 5.304

*The dome in the 1st picture is represented by the color orange.Looking into the second picture, the dome formula derivatives from the volume of a dome of a hemisphere. By using the following linear system:

• triangle_side2 + a2 = r2
• h + triangle_side = r