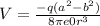Answer:
electric potential, V = -q(a²- b²)/8π∈₀r³
Step-by-step explanation:
Question (in proper order)
Consider two thin coaxial, coplanar, uniformly charged rings with radii a and b (b < a) and charges q and -q, respectively. Determine the potential at large distances from the rings
consider the attached diagram below
the electric potential at point p, distance r from the center of the outer charged ring with radius a is as given below
Va = q/4π∈₀ [1/(a² + b²)¹/²]

Also
the electric potential at point p, distance r from the center of the inner charged ring with radius b is
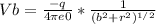
Sum of the potential at point p is
V = Va + Vb
that is
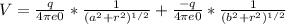
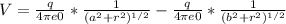
![V = (q)/(4\pi e0) * [(1)/((a^(2) + r^(2) )^(1/2) ) - (1)/((b^(2) + r^(2) )^(1/2) )]](https://img.qammunity.org/2021/formulas/physics/college/74z3j4iwcju3ecliaapokjvg8k9exzpusl.png)
the expression below can be written as the equivalent
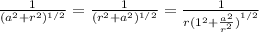
likewise,

hence,
![V = (q)/(4\pi e0) * [\frac{1}{{r(1^(2) + (a^(2) )/(r^(2) ) )}^(1/2) } - \frac{1}{{r(1^(2) + (b^(2) )/(r^(2) ) )}^(1/2) }]](https://img.qammunity.org/2021/formulas/physics/college/t0zjab7x99bgah4axucbm8ctdf4qhhc600.png)
1/r is common to both equation
hence, we have it out and joined to the 4π∈₀ denominator that is outside
![V = (q)/(4\pi e0 r) * [\frac{1}{{(1^(2) + (a^(2) )/(r^(2) ) )}^(1/2) } - \frac{1}{{(1^(2) + (b^(2) )/(r^(2) ) )}^(1/2) }]](https://img.qammunity.org/2021/formulas/physics/college/rd1u6c2rkly3gxr2bccir8mmfddbfw5prp.png)
by reciprocal rule
1/a² = a⁻²
![V = (q)/(4\pi e0 r) * [{(1^(2) + (a^(2) )/(r^(2) ) )}^(-1/2) - {(1^(2) + (b^(2) )/(r^(2) ) )}^(-1/2)]](https://img.qammunity.org/2021/formulas/physics/college/7gszkfkjwml2bvkbfw4pou2an6knziv8hd.png)
by binomial expansion of fractional powers
where
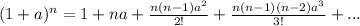
if we expand the expression we have the equivalent as shown
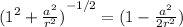
also,
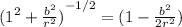
the above equation becomes
![V = (q)/(4\pi e0 r) * [((1-(a^(2) )/(2r^(2) ) ) - (1-(b^(2) )/(2r^(2) ) )]](https://img.qammunity.org/2021/formulas/physics/college/yknggyxphqsxghti5ziybvdlxadv6jhehy.png)
![V = (q)/(4\pi e0 r) * [1-(a^(2) )/(2r^(2) ) - 1+(b^(2) )/(2r^(2) )]](https://img.qammunity.org/2021/formulas/physics/college/cycj56xifafouqhg2vue3hjpzzxglrd5z1.png)
![V = (q)/(4\pi e0 r) * [-(a^(2) )/(2r^(2) ) +(b^(2) )/(2r^(2) )]\\\\V = (q)/(4\pi e0 r) * [(b^(2) )/(2r^(2) ) -(a^(2) )/(2r^(2) )]](https://img.qammunity.org/2021/formulas/physics/college/ne5eagmgyystij5bi2z5ivdq2vuvxeuygj.png)
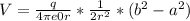

Answer

OR