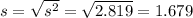Answer:
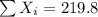
And we can calculate the mean with the following formula:
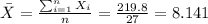
We can calculate the sample variance with this formula:
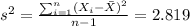
And the sample deviation would be given by:
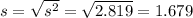
Explanation:
For this case we have the following data given:
7.9 9.7 9.7 8.7 7.0 7.2 11.3 11.8 7.3 8.1 8.0 11.6 6.8 9.0 6.3 7.0 7.4 8.7 6.8 5.8 7.8 7.7 6.3 7.0 7.7 6.5 10.7
Our variable of interest is given by X="flexural strength (MPa) for concrete beams of a certain type"
And for this case we know that
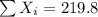
And we can calculate the mean with the following formula:
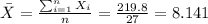
We can calculate the sample variance with this formula:
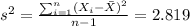
And the sample deviation would be given by: