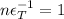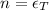Question

For a tensile test, it can be demonstrated that necking begins when dσTdεT=σT. Using Equation σT=K(εT)n, determine an expression for the value of true strain at this onset of necking.

Answer 1

Complete Question

The complete question is shown on the first uploaded image

Answer:

The value of the true strain at the onset of the necking is proved as,
`n = \epsilon_T`

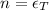
Step-by-step explanation:

From the question we see that necking begins when

`(d \sigma_T)/(d \epsilon_T) = \sigma_T ---(1)`

Now we are told that

`\sigma_T = K \epsilon ^n _T`

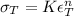
So substituting this into equation 1

`(d)/(d \epsilon_T) (K \epsilon^n_T) = \sigma_T`

`K n \epsilon^(n-1)_T = \sigma_T`

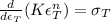
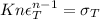
But we are told in the question that
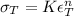`\sigma_T = K \epsilon ^n _T` So,

`K n \epsilon^(n-1)_T = K \epsilon ^n _T`

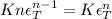
Dividing both sides with
`K \epsilon ^n _T`

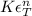
We have

`(K n \epsilon^(n-1)_T)/( K \epsilon ^n _T) =( K \epsilon ^n _T)/(K \epsilon ^n _T)`

`n \epsilon_T^(-1) =1`

`n = \epsilon_T`