Question

The diameter of a segment of an artery is reduced by a factor of two due to an obstruction. Assume that the flow is incompressible and laminar. Compared to an unobstructed segment of the artery, the velocity of blood in the obstructed segment of the artery is __________.

Answer 1

The velocity of blood on an obstructed segment of an artery is greater than an obstructed one

Step-by-step explanation:

The blood as an incompressible an laminar fluid let us to assume the flux of blood in all segments of an artery is the same, this is known as continuity equation and let us to write the change on the flux between some point 1 and some point 2 as:

`\Delta Q = 0`

`Q_2-Q_1=0`

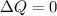
`Q_2=Q_1` (1)

So, if we take the Q1 as the flux on the unobstructed artery and Q2 the obstructed artery, we're saying the flux of blood on the obstructed artery is the same in the unobstructed one. Flux is defined as the velocity of a fluid times the cross-section area on a specific point, so (1) is:

`v_2*A_2=v_1*A_1`

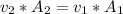
With v the velocity and A the cross-section area, in our should be assumed as a circle of some dimeter D1 and D2 (remember the area of a circle is
`(\pi*D^2)/(4)`)

`v_2*(\pi *D_2^2)/(4)=v_1*(\pi *D_1^2)/(4)`

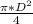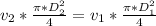
For an obstructed artery D2 is less than D1 and because we have an equality and
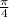`(\pi)/(4)` is constant, v2 should be greater than v1 to conserve the equality, that means the velocity of blood on an obstructed segment of an artery is greater than an obstructed one.