Question

Two solenoids are equal in length and radius, and the cores of both are identical cylinders of iron. However, solenoid A has four times the number of turns per unit length as solenoid B.(a) Which solenoid has the larger self-inductance?A B they are the same(b) What is the ratio of the self-inductance of solenoid A to the self-inductance of solenoid B?LA/LB =______

Answer 1

Step-by-step explanation:

Length of both the solenoids = l

Area of crossection of both the solenoids = A

Current in both the solenoids = i

Let the number of turns in coil A is 4N and the number of turns in coil B is N.

The self inductance due to the long solenoid is given by

`L = (\mu_(0)N^(2)A)/(l)`

As the current, area of crossection and the length is same so

`(L_(A))/(L_(B))=(N_(A)^(2))/(N_(B)^(2))`

`(L_(A))/(L_(B))=(16N^(2))/(N^(2))`

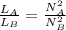
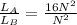
So, LA : LB = 16 : 1

Answer 2

`(L_A)/(L_B)=16`

Step-by-step explanation:

`\mu_0` = Vacuum permeability =
`4\pi * 10^(-7)\ H/m`

n = Number of turns

A = Area

I = Current

Self inductance is given by

`L=\mu_0n^2IA`

Here, A has more turns so the self-inductance of A will be higher

For A

`L_A=\mu_0n_A^2IA=\mu_0(4n_B)^2IA`
`[\because n_A=4n_B]`

For B

`L_B=\mu_0n_B^2IA`

Dividing the above two equations we have

`(L_A)/(L_B)=(\mu_0(4n_B)^2IA)/(\mu_0n_B^2IA)\\\Rightarrow (L_A)/(L_B)=16`

`\therefore (L_A)/(L_B)=16`