Question

What are the coordinates of the point on the directed line segment from (-9, -1)(−9,−1) to (-9, -10)(−9,−10) that partitions the segment into a ratio of 2 to 1?

Answer 1

Therefore the co-ordinate of the point on the line segment from (-9,-1) to(-9,-10) into a ratio internally is (-9,-7).

Therefore the co-ordinate of the point on the line segment from (-9,-1) to(-9,-10) into a ratio internally is (-9,-19).

Explanation:

Given points are (-9,-1) and (-9,-10)

If a point divides the line segment by joining two points (x₁,y₁) and (x₂,y₂) into a ratio m:n internally.

Then the point of the coordinate is
`((m.x_2+nx_1)/(m+n),(my_2+ny_1)/(m+n))`.

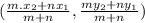If a line segment is externally divided into a point by joining two points (x₁,y₁) and (x₂,y₂) with m: n ratio.

Then the point of the coordinate is
`((m.x_2-nx_1)/(m-n),(my_2-ny_1)/(m-n))`.

Internally

The co-ordinate of the point is
`(((-9)*2+(-9)* 1)/(2+1),((-10)* 2+(-1)* 1)/(2+1))`

`=(-9,-7)`

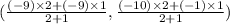
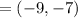
Externally

The co-ordinate of the point is
`(((-9)*2-(-9)* 1)/(2-1),((-10)* 2-(-1)* 1)/(2-1))`

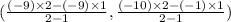
= (-9,-19)