Answer:
When the radius is 11 feet, the area is changing at approximately 276.571 square feet per minute.
Explanation:
We are given the following in the question:
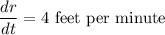
Instant radius = 11 feet
Area of circle =
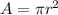
where r is the radius of the circle.
Rate of change of area of circle =

Putting all the values, we get,
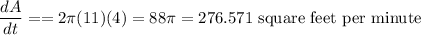
Thus, when the radius is 11 feet, the area is changing at approximately 276.571 square feet per minute.