Question

A survey of 1050 eligible voters, an approximate 98% confidence interval estimate for the proportion of voters who claimed to have voted in the last presidential election was (0.616, 0.681).

Answer 1

There is a 98% confidence that the true proportion of voters who have voted in the last presidential election lies in this interval.

Explanation:

The confidence interval for estimating the population proportion is:

`CI=\hat p\pm z_(\alpha/2)\sqrt{(\hat p(1-\hat p))/(n)}`

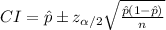
The 98% confidence interval estimate for the proportion of voters who claimed to have voted in the last presidential election was (0.616, 0.681).

The sample taken was of size, n = 1050.

Interpretation:

The 98% confidence interval (0.616, 0.681) for the proportions of voters who claimed to have voted in the last presidential election implies that the true proportion of voters who have voted lies in this interval with 0.98 probability.

Or, there is a 98% confidence that the true proportion of voters who have voted in the last presidential election lies in this interval.

Or, if 100 such samples are taken and 100 such 98% confidence interval are made then 98 of these confidence intervals would consist of the true proportion of voters who have voted in the last presidential election.