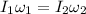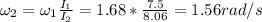Answer:
1.56 rad/s
Step-by-step explanation:
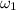 = 16 revolution/minute = 16 * 2π (rad/rev) * (1/60) (min/sec) = 1.68 rad/s
= 16 revolution/minute = 16 * 2π (rad/rev) * (1/60) (min/sec) = 1.68 rad/s
46 cm = 0.46 m
Treating the lump of clay as a point mass 46 cm from the rotational axis, the new rotational inertia of the system would be

According the the law of momentum conservation, the product of rotational inertia and angular speed must stay the same: