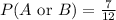Sets A and B are independent events and are mutually exclusive P(A)= 1/4 and P(B)= 1/3 P(A and B)= P(A or B)=

Question

asked Jul 25, 2021 64.3k views

1 Answer

Arivan Bastos · Answer 1 · 2021-07-30T20:02:25+0000

The solutions are
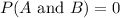${P}({A} \text { and }B})=0$ and
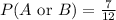
$P}({A} \text { or } {B})=(7)/(12)$

Step-by-step explanation:

Given that the sets A and B are independent events and are mutually exclusive events.

We need to determine the value of
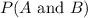$P(A \text { and } B)$ and
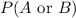
$P(A \text { or } B)$

The value of
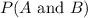$P(A \text { and } B)$ :

Since, the sets A and B are mutually exclusive events, it is impossible for the two events to occur together.

Hence, we have,

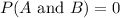
${P}({A} \text { and }B})=0$

Thus, the value of
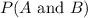$P(A \text { and } B)$ is 0.

The value of
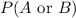$P(A \text { or } B)$ :

For mutually exclusive events, the value of
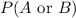$P(A \text { or } B)$ is given by the formula,

$P(A \text { or } B)=P(A)+P(B)$

Substituting the values, we get,

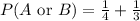
$P(A \text { or } B)=(1)/(4)+(1)/(3)$

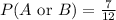
$P}({A} \text { or } {B})=(7)/(12)$

Hence, the value of
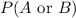$P(A \text { or } B)$ is
(7)/(12)

Thus, the solutions are
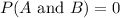${P}({A} \text { and }B})=0$ and
$P}({A} \text { or } {B})=(7)/(12)$