Question

The position of a particle is given i(t) = A(coswt i + sin wt 1), where w is a constant. (a) Show that the particle moves in a circle of radius A. (b) Calculate and then show that the speed of the particle is a constanta (c) Determine and show that a is given by ae = rw?. (d) Calculate the centripetal force on the particle.

Answer 1

Step-by-step explanation:

(a) we can prove that the particle moves in a circle by taking the square of the norm of r(t)

`|r(t)|=\sqrt{A^(2)[cos^(2)(\omega t)+sin^(2)(\omega t)]}\\cos^(2)(\omega t)+sin^(2)(\omega t)=1\\|r(t)|=A\\r=A`

the norm of the position vector does not depend of time, so |r| is constant and is a radius of a circle.

(b) the sped of the particle is the norm of the velocity v(t). Velocity is calculated by derivating r(t)

`v(t)=(dr(t))/(dt)=A(-\omega sin(\omega t)\hat{i}+\omega cos(\omega t)\hat{j})\\|v(t)|=\sqrt{A^(2)\omega^(2)(sin^(2)(\omega t)+cos^(2)(\omega t))}\\v=A\omega`

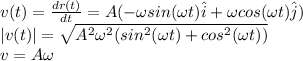
A and w are constant, hence the speed of the particle is constant.

(c) the acceleration is the derivative of the velocity

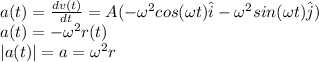
`a(t)=(dv(t))/(dt)=A(-\omega ^(2)cos(\omega t)\hat{i}-\omega^(2)sin(\omega t)\hat{j})\\ a(t)=-\omega^(2)r(t)\\|a(t)|=a=\omega^(2)r`

(d)

`F_(c)=ma_(c)=m(v^(2))/(r)=m(A^(2)\omega ^(2))/(A)=mA\omega ^(2)`

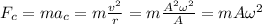
I hope this is useful for you

regards