Answer:
96% confidence interval estimate for the mean monthly rent of all unmarried BYU students in winter 2018 is [335.89 , 356.10].
Explanation:
We are given that a group of researchers at the BYU Off-Campus Housing department want to estimate the mean monthly rent that unmarried BYU students paid during winter 2018.
During March 2018, they randomly sampled 314 BYU students and found that on average, students paid $346 for rent with a standard deviation of $86.
So, the pivotal quantity for 95% confidence interval for the average age is given by;
P.Q. =
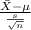 ~
~
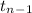
where,
 = average rent paid by 314 BYU students = $346
= average rent paid by 314 BYU students = $346
s = sample standard deviation = $86
n = sample of students = 314
 = population mean monthly rent of all unmarried BYU students
= population mean monthly rent of all unmarried BYU students
So, 96% confidence interval for the population mean monthly rent,
 is ;
is ;
P(-2.082 <
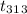 < 2.082) = 0.96
< 2.082) = 0.96
P(-2.082 <
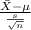 < 2.082) = 0.96
< 2.082) = 0.96
P(
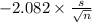 <
<
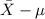 <
<
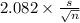 ) = 0.96
) = 0.96
P(
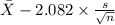 <
<
 <
<
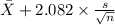 ) = 0.96
) = 0.96
96% confidence interval for
 = [
= [
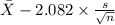 ,
,
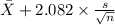 ]
]
= [
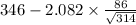 ,
,
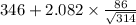 ]
]
= [335.89 , 356.10]
Therefore, 96% confidence interval estimate for the mean monthly rent of all unmarried BYU students in winter 2018 is [335.89 , 356.10].