Answer:
0.17 is the probability that X takes a value less than 158.
Explanation:
We are given the following in the question:
Mean = 169
The variable X is normally distributed.
Formula:



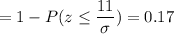
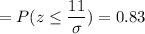
Calculation the value from standard normal z table, we have,
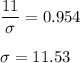
We have to evaluate
P(x < 158)
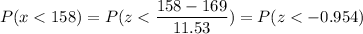
Calculation the value from standard normal z table, we have,

0.17 is the probability that X takes a value less than 158.