Answer:
The probability that the first to arrive waits no longer than 15 minutes is 1/3
Explanation:
Let X be the distribution of time where the man arrives and Y the distribution for the woman. Since it is a 40 minute period, the density function of X is
![f_X(t) = 1/40 \, I_([11:30, 12:10])](https://img.qammunity.org/2021/formulas/mathematics/college/uhw4pyiuuonfdi8vyef9wu73vdexi7s83c.png)
(Note: it is weird not to work with real numbers, however, you can think an hour as 60 minutes; for example 11:30 = 11*60+30 = 690, so we are working with real numbers after all. But it is more comfortable to work with minutes and hour notation)
The density of Y is
![f_Y(t) = 1/45 \, I_([11:50, 12:35])](https://img.qammunity.org/2021/formulas/mathematics/college/dwwid09vjhosuj0i957rw8cx9mij7si54e.png)
Note that if the man arrives at 11:30, he will have to wait more than 15 minutes regardless of when the woman arrives; he has to arrive at least 11:35 for a chance. The same way, no matter how late the man arrives, he will wait more than 15 minutes if the woman arrives after 12:25
We can obtain the desired probability spltting the event in 2: when the man arrives earlier and when the woman does. For the first even we need to integrate the product of the density functions (which are independent), with X taking any value greater than 11:35 until 12:10 and Y being between X and X+15. Then we integrate with X between 11:50 + 15 = 12:05 and 12:10 and Y between X-15 and X

Now,
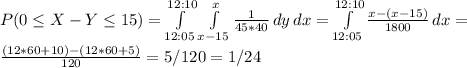
And,
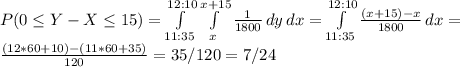
Thus, P(|X-Y| ≤ 15) = 1/24 + 7/24 = 1/3.
The probability that the first to arrive waits no longer than 15 minutes is 1/3.