Question

Suppose that a histogram of a data set is approximately symmetric and "bell shaped". Approximately what percent of the observations are within one standard deviation of the mean?

Answer 1

Suppose that a histogram of a data set is approximately symmetric and "bell shaped". approximately what percent of the observations are within one standard deviation of the mean?

a. 99.7%

b. 50%

c. 68%

d. 95%

Option c is the right choice where, 68% of the observations are within 1 standard deviation.

Explanation:

Given :

Standard deviation of the population =
`\sigma`

Average value for the population,(mean) =
`\mu`

Score or the data point to be converted =
`x`

So,

Z-score formula =
`(x-\mu)/(\sigma)`

If the Z-score is positive, it means the score is above the average value, whereas a negative Z-score indicates the score is below the average.

According to the question within 1 standard deviation (SD) of the mean is the
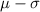`\mu-\sigma` to
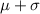`\mu+\sigma` values from the bell shaped diagram.

One of a diagram is attached below.

And

The 68-95-99.7 Rule/Three sigma rule/Empirical rule states that, for normally distributed samples:

• This rule is often used in statistics for forecasting.
• 68% of the measures are within one standard deviation of the mean.
• 95% fall within two standard deviations.
• 99.7% fall within three standard deviations.

So,

Our final answer is of 68%,as of the measures are with in one SD.