Question

A 0.140 kg stone rests on a frictionless, horizontal surface. A bullet of mass 8.50 g , traveling horizontally at 320 m/s , strikes the stone and rebounds horizontally at right angles to its original direction with a speed of 250 m/s.

(a) Compute the magnitude and direction of the velocity of the stone after it is struck.
(b) Is the collision perfectly elastic?

Answer 1

a)
`v = 34.607\,(m)/(s)` (Positive), b)
`e = 0.803`. The collision is not perfectly elastic.

Step-by-step explanation:

a) The collision can be described by the Principle of Momentum Conservation and Principle of Energy Conservation:

`(0.140\,kg)\cdot (0\,(m)/(s) ) + (0.0085\,kg)\cdot (320\,(m)/(s) ) = (0.0085\,kg)\cdot (-250\,(m)/(s) ) + (0.140\,kg)\cdot v`

The final velocity of the rock is:

`v = 34.607\,(m)/(s)`

b) The coefficient of restitution is the best criterion to distinguish elastic collsions from inelastic collisions, such criterion is the ratio of final energy of the system to initial energy of the system:

`e = ((1)/(2)\cdot [(0.140\,kg)\cdot (34.607\,(m)/(s) )^(2)+(0.0085\,kg)\cdot (-250\,(m)/(s) )^(2)] )/((1)/(2)\cdot [(0.140\,kg)\cdot (0\,(m)/(s) )^(2)+(0.0085\,kg)\cdot (320\,(m)/(s) )^(2)] )`

`e = 0.803`

The collision is not perfectly elastic.

Answer 2

a) magnitude of the stone's velocity = 24.66 m/s

Direction = - 38⁰

b) The collision is not perfectly elastic

Step-by-step explanation:

The mass of the stone,
`m_(s) = 0.140 kg`

The mass of the bullet,
`m_(b) = 8.50 g = 0.0085 kg`

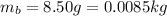
The initial speed of the bullet before striking the stone,
`v_(b1) = 320i m/s`

The final speed of the bullet after rebound,
`v_(b2) = 250j m/s`

The initial speed of the stone before collision,
`v_(s1) = 0 m/s`

The final velocity of the stone in the x- direction,
`v_(s2) = ?`

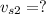
a) In the x - direction,
`v_(b2) =0 m/s`

Since momentum is conserved before and after collision:

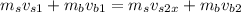`m_(s) v_(s1) +m_(b) v_(b1) = m_(s) v_(s2x) +m_(b) v_(b2)`..................(1)

`(0.14*0) + (0.0085 * 320) = (0.14 * v_(s2x) ) + (0.0085*0)\\0.14 * v_(s2x) = 0.0085 * 320\\v_(s2x) = (2.72)/(0.14) \\v_(s2x) = 19.43 m/s`

In the y - direction,
`v_(s1) =0, v_(b1) =0`,
`v_(b2) = 250 m/s`

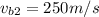
Inserting these values into equation (1)

`(0.14*0) + (0.0085*0) = (0.14*v_(s2y) ) + (0.0085*250)\\0.14*v_(s2y) = -2.125\\v_(s2y) = (-2.125)/(0.14) \\v_(s2y) = -15.18 m/s`

Magnitude of the velocity of the stone:

`v_(s2) = \sqrt{v_(s2x) ^(2) +v_(s2y) ^(2)} \\v_(s2) = \sqrt{19.43 ^(2) +(-15.18) ^(2)}\\v_(s2) = 24.66 m/s`

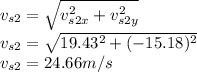
Direction of the velocity of the stone:

`\theta = tan^(-1) (v_(s2y) )/(v_(s2x) ) \\\theta = tan^(-1) (-15.18 )/(19.43 ) \\\theta = - 38^(o)`

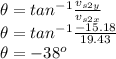
b) The collision is perfectly elastic if :

`v_(s1) - v_(b1) = v_(b2) - v_(s2) \\v_(s1) - v_(b1) = 0 - 350 i\\v_(s1) - v_(b1) = (-350 m/s) i\\ v_(b2) - v_(s2) = 250j - (19.43i - 15.18 j)\\ v_(b2) - v_(s2) = -19.43i + 265.18j`

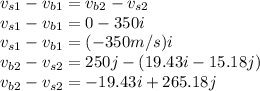
Since
`v_(s1) - v_(b1) \\eq v_(b2) - v_(s2)`

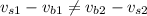
the collision is not perfectly elastic