Question

The world population at the beginning of 1980 was 4.5 billion. Assuming that the population continued to grow at the rate of approximately 1.3%/year, find a function Q that expresses the world population (in billions) as a function of time t (in years). (Let t = 0 represent 1980 where t is years since 1980.)

What does Q(t) = and what will the world population be at the beginning of 2019 ?

Answer 1

`Q(t) = 4.5(1.013)^(t)`

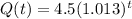
The world population at the beginning of 2019 will be of 7.45 billion people.

Explanation:

The world population can be modeled by the following equation.

`Q(t) = Q(0)(1+r)^(t)`

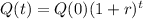
In which Q(t) is the population in t years after 1980, in billions, Q(0) is the initial population and r is the growth rate.

The world population at the beginning of 1980 was 4.5 billion. Assuming that the population continued to grow at the rate of approximately 1.3%/year.

This means that
`Q(0) = 4.5, r = 0.013`

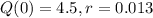
So

`Q(t) = Q(0)(1+r)^(t)`

`Q(t) = 4.5(1.013)^(t)`

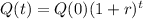
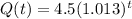
What will the world population be at the beginning of 2019 ?

2019 - 1980 = 39. So this is Q(39).

`Q(t) = 4.5(1.013)^(t)`

`Q(39) = 4.5(1.013)^(39) = 7.45`

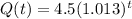
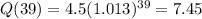
The world population at the beginning of 2019 will be of 7.45 billion people.