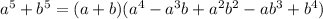Question

Calculus, question 5 to 5a​

Answer 1

5. Let
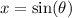`x = \sin(\theta)`. Note that we want this variable change to be reversible, so we tacitly assume 0 ≤ θ ≤ π/2. Then

`\cos(\theta) = √(1 - \sin^2(\theta)) = √(1 - x^2)`

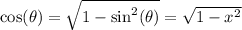
and
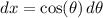`dx = \cos(\theta) \, d\theta`. So the integral transforms to

`\displaystyle \int (x^3)/(√(1-x^2)) \, dx = \int (\sin^3(\theta))/(\cos(\theta)) \cos(\theta) \, d\theta = \int \sin^3(\theta) \, d\theta`

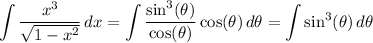
Reduce the power by writing

`\sin^3(\theta) = \sin(\theta) \sin^2(\theta) = \sin(\theta) (1 - \cos^2(\theta))`

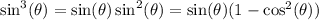
Now let
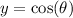`y = \cos(\theta)`, so that
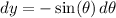`dy = -\sin(\theta) \, d\theta`. Then

`\displaystyle \int \sin(\theta) (1-\cos^2(\theta)) \, d\theta = - \int (1-y^2) \, dy = -y + \frac13 y^3 + C`

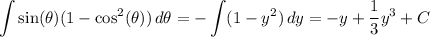
Replace the variable to get the antiderivative back in terms of x and we have

`\displaystyle \int (x^3)/(√(1-x^2)) \, dx = -\cos(\theta) + \frac13 \cos^3(\theta) + C`

`\displaystyle \int (x^3)/(√(1-x^2)) \, dx = -√(1-x^2) + \frac13 \left(√(1-x^2)\right)^3 + C`

`\displaystyle \int (x^3)/(√(1-x^2)) \, dx = -\frac13 √(1-x^2) \left(3 - \left(√(1-x^2)\right)^2\right) + C`

`\displaystyle \int (x^3)/(√(1-x^2)) \, dx = \boxed{-\frac13 √(1-x^2) (2+x^2) + C}`

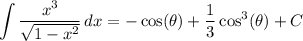
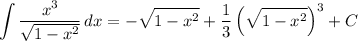
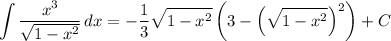
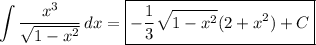
6. Let
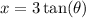`x = 3\tan(\theta)` and
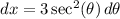`dx=3\sec^2(\theta)\,d\theta`. It follows that

`\cos(\theta) = \frac1{\sec(\theta)} = \frac1{√(1+\tan^2(\theta))} = \frac3{√(9+x^2)}`

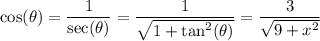
since, like in the previous integral, under this reversible variable change we assume -π/2 < θ < π/2. Over this interval, sec(θ) is positive.

Now,

`\displaystyle \int (x^3)/(√(9+x^2)) \, dx = \int (27\tan^3(\theta))/(√(9+9\tan^2(\theta))) 3\sec^2(\theta) \, d\theta = 27 \int (\tan^3(\theta) \sec^2(\theta))/(√(1+\tan^2(\theta))) \, d\theta`

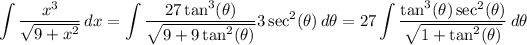
The denominator reduces to

`√(1+\tan^2(\theta)) = √(\sec^2(\theta)) = |\sec(\theta)| = \sec(\theta)`

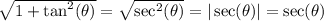
and so

`\displaystyle 27 \int \tan^3(\theta) \sec(\theta) \, d\theta = 27 \int (\sin^3(\theta))/(\cos^4(\theta)) \, d\theta`

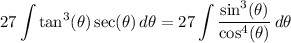
Rewrite sin³(θ) just like before,

`\displaystyle 27 \int (\sin(\theta) (1-\cos^2(\theta)))/(\cos^4(\theta)) \, d\theta`

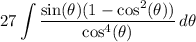
and substitute
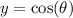`y=\cos(\theta)` again to get

`\displaystyle -27 \int (1-y^2)/(y^4) \, dy = 27 \int \left(\frac1{y^2} - \frac1{y^4}\right) \, dy = 27 \left(\frac1{3y^3} - \frac1y\right) + C`

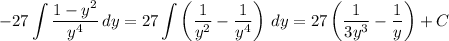
Put everything back in terms of x :

`\displaystyle \int (x^3)/(√(9+x^2)) \, dx = 9 \left(\frac1{\cos^3(\theta)} - \frac3{\cos(\theta)}\right) + C`

`\displaystyle \int (x^3)/(√(9+x^2)) \, dx = 9 \left((\left(√(9+x^2)\right)^3)/(27) - √(9+x^2)\right) + C`

`\displaystyle \int (x^3)/(√(9+x^2)) \, dx = \boxed{\frac13 √(9+x^2) (x^2 - 18) + C}`

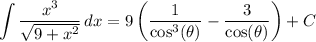
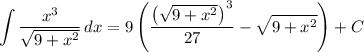
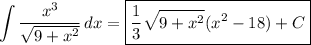
2(b). For some constants a, b, c, and d, we have

`\frac1{x^2+x^4} = \frac1{x^2(1+x^2)} = \boxed{\frac ax + \frac b{x^2} + (cx+d)/(x^2+1)}`

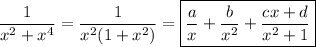
3(a). For some constants a, b, and c,

`(x^2+4)/(x^3-3x^2+2x) = (x^2+4)/(x(x-1)(x-2)) = \boxed{\frac ax + \frac b{x-1} + \frac c{x-2}}`

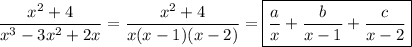
5(a). For some constants a-f,

`(x^5+1)/((x^2-x)(x^4+2x^2+1)) = (x^5+1)/(x(x-1)(x+1)(x^2+1)^2) \\\\ = (x^4 - x^3 + x^2 - x + 1)/(x(x-1)(x^2+1)^2) = \boxed{\frac ax + \frac b{x-1} + (cx+d)/(x^2+1) + (ex+f)/((x^2+1)^2)}`

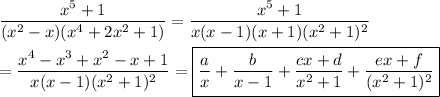
where we use the sum-of-5th-powers identity,

`a^5 + b^5 = (a+b) (a^4-a^3b+a^2b^2-ab^3+b^4)`