Question

The differential equation dy dx equals the quotient of the quantity x minus 2 and y minus 2. produces a slope field with horizontal tangents at y = 2 produces a slope field with vertical tangents at y = 2 produces a slope field with columns of parallel segments\

Answer 1

The curve produces a slope field with vertical tangents at y = 2.

Explanation:

The differential equation
`(dy)/(dx)` equals the quotient of the quantity x minus 2 and y minus 2.

Hence,
`(dy)/(dx) = (x - 2)/(y - 2)`

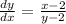
Now, at y = 2,
`(dy)/(dx)` becomes ∞ and hence the curve y = f(x) with
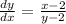`(dy)/(dx) = (x - 2)/(y - 2)` will have tangents at y = 0 with slopes equal to ∞ i.e. the tangents make 90° angle with the positive x-axis.

Therefore, the curve produces a slope field with vertical tangents at y = 2. (Answer)