Question

The population of a town grows at a rate proportional to the population present at time t. The initial population of 500 increases by 25% in 10 years. What will be the population in 20 years

Answer 1

The population in 20 years will be 781.

Explanation:

The population of the town can be modeled by the following equation:

`P(t) = P(0)e^(rt)`

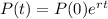
In which P(t) is the population after t years, P(0) is the initial population and r is the growth rate, as a decimal.

The initial population of 500 increases by 25% in 10 years.

This means that
`P(0) = 500, P(10) = 1.25*P(0) = 625`

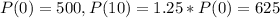
We use this to find r.

`P(t) = P(0)e^(rt)`

`625 = 500e^(10r)`

`e^(10r) = 1.25`

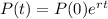
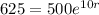
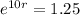
Applying ln to both sides

`\ln{e^(10r)} = ln(1.25)`

`10r = ln(1.25)`

`r = (ln(1.25))/(10)`

`r = 0.0223`

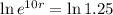
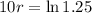
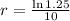
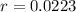
So

`P(t) = 500e^(0.0223t)`

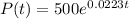
What will be the population in 20 years

This is P(20)

`P(20) = 500e^(0.0223*20) = 781`

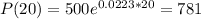
The population in 20 years will be 781.