Question

The probability that a person will have 0, 1, or 2 dental checkups per year is 0.3, 0.6, and 0.1, respectively. If seven people are picked at random, what is the probability that two will have no checkups, four will have one checkup, and one will have two checkups in the next year?

A) 0.012
B) 0.122
C) 0.588
D) 0.018

Answer 1

The required probability is 0.1224.

Explanation:

Here, given:

The probability of having 0 dental checkup = 0.3

The probability of having 1 dental checkup = 0.6

The probability of having 2 dental checkup = 0.1

Number of people chosen at random = 7

So, the number of ways 2, 4 and 1 checkup are :
`((7!)/(2! * 4! * 1!) )`

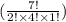
Now, the combined probability that two will have no checkups, four will have one checkup, and one will have two checkups in the next year

=
`((7!)/(2! * 4! * 1!) ) * (0.3)^2 * (0.6)^4 * (0.1)^1 = 0.1224`

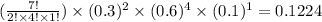
Hence, the required probability is 0.1224.