1 Answer

Agregoire · Answer 1 · 2021-08-13T03:34:53+0000

Answer:

a) If
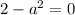2-a^(2)=0 and
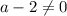$a-2\\eq 0$ . The system has no solution

b) If
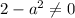$2-a^(2)\\eq 0$ and a different to 2, we have a unique solution.

c) If
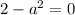2-a^(2)=0 and
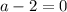a-2=0 we have infinitely solutions.

Explanation:

We need to rewrite the third equation in terms of a and z to solve this.

Let's start solving the first equation:

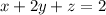x+2y+z=2 (1)

If we subtract z in both side of this equation we will have:

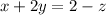x+2y=2-z (2)

Now we can put the equation 2 into the last equation:

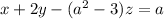
x+2y-(a^(2)-3)z=a

2-z-(a^(2)-3)z=a (3)

Simplifying the equation 3 we have:

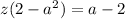z(2-a^(2))=a-2 (4)

Now we can analyzes the equation 4 for each case:

a) If
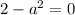2-a^(2)=0 and
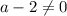$a-2\\eq 0$ . The system has no solution

b) If
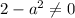$2-a^(2)\\eq 0$ and a different to 2, we have a unique solution.

c) If
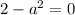2-a^(2)=0 and
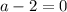a-2=0 we have infinitely solutions.

I hope it helps you!

Please log in or register to add a comment.