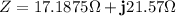Question

An open-circuit experiment is conducted on the low-voltage side of a 200 kVA, 4000 V/220 V, single-phase transformer in its nominal frequency. The open-circuit voltage is 220 V and the open-circuit current and power are 8 A and 1100 W, respectively. Find the shunt impedance of the transformer referred to its low voltage side

Answer 1

`Z=17.1875\Omega +\mathbf{j}21.57\Omega`

Step-by-step explanation:

Alternating Current Circuit

The circuit parameters in an AC circuit are complex numbers to express the phase and magnitude components of currents, voltages, powers, and impedances.

The impedance is the equivalent to the resistance in direct current and has two components: the active R and the reactive X. It's expressed as

`Z=R+\mathbf{j}X`

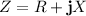
Where j is the unit component of the complex numbers

`\mathbf{j}=√(-1)`

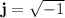
The equations for direct current stand for alternating current but taking the parameters as complex numbers.

We are given some data to compute the shunt impedance of the transformer: The open-circuit voltage magnitude is 220 V, the active power P=1100W and the magnitude of the current I=8 A

The active power is the power dissipated by the resistance:

`P=I^2R`

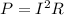
Solving for R

`\displaystyle R=(P)/(I^2)=(1100)/(8^2)=17.1875 \Omega`

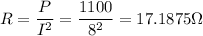
Now we know the magnitude of the impedance Z is

`\displaystyle |Z|=(|V|)/(|I|)=(220)/(8)=27.5\Omega`

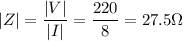
Since

`Z^2=R^2+X^2`

Solving for X

`X=√(Z^2-R^2)=√(27.5^5-17.1875^2)=21.47\Omega`

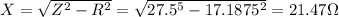
Thus, the shunt impedance is

`Z=17.1875\Omega +\mathbf{j}21.57\Omega`