Question

For the cost function c equals 0.1 q squared plus 2.1 q plus 8​, how fast does c change with respect to q when q equals 11​? Determine the percentage rate of change of c with respect to q when q equals 11.

Answer 1

Rate of change of c with respect to q is 4.3

Percentage rate of change c with respect to q is 9.95%

Explanation:

Cost function is given as,
`c=0.1\:q^(2)+2.1\:q+8`

Given that c changes with respect to q that is,
`(dc)/(dq)`. So differentiating given function,

`(dc)/(dq)=(d)/(dq)\left (0.1\:q^(2)+2.1\:q+8 \right)`

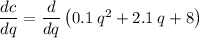
Applying sum rule of derivative,

`(dc)/(dq)=(d)/(dq)\left(0.1\:q^(2)\right)+(d)/(dq)\left(2.1\:q\right)+(d)/(dq)\left(8\right)`

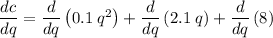
Applying power rule and constant rule of derivative,

`(dc)/(dt)=0.1\left(2\:q^(2-1)\right)+2.1\left(1\right)+0`

`(dc)/(dt)=0.1\left(2\:q\right)+2.1`

`(dc)/(dt)=0.2\left(q\right)+2.1`

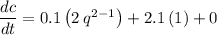
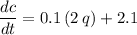
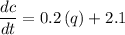
Substituting the value of
`q=11`,

`(dc)/(dt)=0.2\left(11\right)+21.`

`(dc)/(dt)=2.2+2.1`

`(dc)/(dt)=4.3`

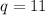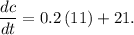
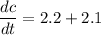
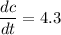
Rate of change of c with respect to q is 4.3

Formula for percentage rate of change is given as,

`Percentage\:rate\:of\:change=(Q'\left(x\right))/(Q\left(x\right))* 100`

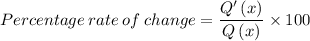
Rewriting in terms of cost C,

`Percentage\:rate\:of\:change=(C'\left(q\right))/(C\left(q\right))* 100`

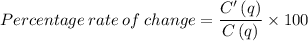
Calculating value of
`C\left(q \right)`

`C\left(q\right)=0.1\:q^(2)+2.1\:q+8`

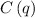
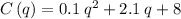
Substituting the value of
`q=11`,

`C\left(q\right)=0.1\left(11\right)^(2)+2.1\left(11\right)+8`

`C\left(q\right)=0.1\left(121\right)+23.1+8`

`C\left(q\right)=12.1+23.1+8`

`C\left(q\right)=43.2`

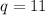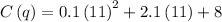
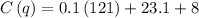
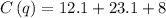
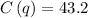
Now using the formula for percentage,

`Percentage\:rate\:of\:change=(4.3)/(43.2)* 100`

`Percentage\:rate\:of\:change=0.0995* 100`

`Percentage\:rate\:of\:change=9.95%`

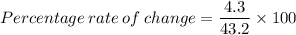
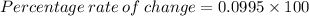
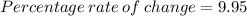
Percentage rate of change of c with respect to q is 9.95%