Question

A study on students drinking habits wants to determine the true average number of alcoholic drinks all FSU undergraduate students who are members of a fraternity or sorority have in a one week period. We know from preliminary studies that the standard deviation is around 2.6. How many students should be sampled to be within 0.25 drinks of population mean with 95% probability? Group of answer choices 416 415 103 104

Answer 1

The sample size should be n=416 students.

Explanation:

Hello!

The researchers wish to know which sample size should he take to estimate the true average number of alcoholic drinks all FSU undergraduate students who are members of a fraternity or sorority have in one week period.

The study variable is then

X: Number of drinks per week an undergraduate sorority/fraternity member has.

Preliminary studies show that the standard deviation is σ= 2.6 drinks per week.

Using a 1 - α: 0.95 of probability you have to find the sample size to estimate the population mean for a confidence interval with a margin error of no more than d= 0.25

Assuming that the variable has a normal distribution, the best statistic to use for the confidence interval is the standard normal, then the formula for the interval is:

X[bar] ±
`Z_(1-\alpha /2)` *
`(Sigma)/(√(n) )`

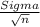
Where the margin of error is:

d=
`Z_(1-\alpha /2)` *
`(Sigma)/(√(n) )`

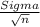
Using the given indormation you have to clear the sample size:

`(d)/( Z_(1-\alpha /2))`=
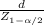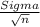
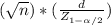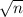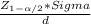
`(Sigma)/(√(n) )`

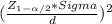
`(√(n) )*((d)/( Z_(1-\alpha /2)))`= Sigma

`√(n)`=
`(Z_(1-\alpha /2)*Sigma)/(d)`

n=
`((Z_(1-\alpha /2)*Sigma)/(d))^2`

n=
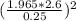`((1.965*2.6)/(0.25))^2`= 415.50

Now since you cannot take a sample of 415.50 students, you have to round it to the next integer, so the sample size the researcher should take is 416 students.

I hope it helps!