Question

Squids and octopuses propel themselves by expelling water. They do this by keeping water in a cavity and then suddenly contracting the cavity to force out the water through an opening. A 6.00 kg squid (including the water in the cavity) at rest suddenly sees a dangerous predator.If the squid has 1.85 kg of water in its cavity, at what speed must it expel this water to instantaneously achieve a speed of 2.70 m/s to escape the predator? Neglect any drag effects of the surrounding water.

Answer 1

The speed of water must be expelled at 6.06 m/s

Step-by-step explanation:

Neglecting any drag effects of the surrounding water we can assume the linear momentum in this case is conserves, that is, the total initial momentum of the octopus and the water kept in it cavity should be equal to the total final linear momentum. That's known as conservation of momentum, mathematically expressed as:

`p_f=p_i`

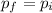
with Pi the total initial momentum and Pf the final total momentum. The total momentum is the sum of the momentums of the individual objects, in our case the octopus and the mass of water that will be expelled:

`p_(of)+p_(wf)=p_(oi)+p_(wi)`

with Po the momentum of the octopus and Pw the momentum of expelled water. Linear momentum is defined as mass times velocity:

`m_o*v_(of)+m_w*v_(wf)=m_o*v_(oi)+m_w*v_(wi)`

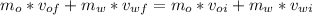
Note that initially the octopus has the water in its cavity and both are at rest before it sees the predator so
`v_(oi)=v_(wi) = 0(m)/(s)`:

`m_o*v_(of)+m_w*v_(wf)=0`

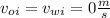We should find the final velocity of water if the final velocity of the octopus is 2.70 m/s, solving for
`v_(wf)`:

`v_(wf)=-(m_o*v_(of))/(m_w)=-((6.00-1.85)*(2.70))/(1.85)`

`v_(wf)=-6.06(m)/(s)`

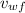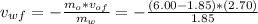
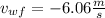
The minus sign indicates the velocity of the water is opposite the velocity of the octopus.