Question

Best Electronics Inc. offers a "no hassle" returns policy. The daily number of customers returning items follows the normal distribution. The mean number of customers returning items is 10.3 per day and the standard deviation is 2.25 per day. A. For any day, what is the probability that eight or fewer customers returned items?

Answer 1

0.1534 is the probability that eight or fewer customers returned items.

Explanation:

We are given the following information in the question:

Mean, μ = 10.3 per day

Standard Deviation, σ = 2.25 per day

We are given that the distribution of daily number of customers returning items is a bell shaped distribution that is a normal distribution.

Formula:

`z_(score) = \displaystyle(x-\mu)/(\sigma)`

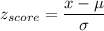
P( eight or fewer customers returned items)

`P( x \leq 8) = P( z \leq \displaystyle(8 - 10.3)/(2.25)) = P(z \leq -1.022)`

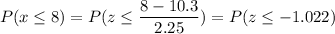
Calculation the value from standard normal z table, we have,

`P(x \leq -1.022) =0.1534= 15.34\%`

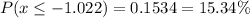
0.1534 is the probability that eight or fewer customers returned items.